SANGRE DE TIERRA

Hace unos cinco siglos, Leonardo da Vinci examinó el río Arno, probablemente por un plan 'ideado con Niccolò Machiavelli' para desviar el importante canal de Pisa a Florencia.

Su gran plan nunca se llevó a cabo. Pero en algún momento del proceso, Da Vinci imaginó cómo sería todo el sistema hidrológico desde arriba. 
Dibujó el tallo principal del Arno, que se dividió en ramas aguas corriente hacia arriba. Luego esas ramas se ramificaron, y así sucesivamente, expandiéndose en pequeñas venas de araña que alimentaban toda la red.

Para Da Vinci, este patrón parecía sospechosamente vivo.

Las redes de ríos, escribió, eran un sistema circulatorio separado, uno que llevaba la "sangre de la Tierra".

Hoy en día, las redes fluviales ramificadas aún atraen a los posibles explicadores, muchos de los cuales esperan vislumbrar algunos códigos matemáticos subyacentes responsables de grabar estos patrones comunes.

No es una hazaña fácil.

Los geomorfólogos han medido durante mucho tiempo las leyes estadísticas de que las redes fluviales parecen obedecer a "la corriente más larga que serpentea a través de una cuenca", por ejemplo, parece ser proporcional al área de la cuenca elevada a la potencia de 0.6.

Pero estas leyes genéricas no han ofrecido mucha información sobre lo que realmente da forma a las redes. 
Otro problema es que el mundo real no escatima en detalles. La cantidad de lluvia, los recovecos y grietas en los que cae la lluvia, los sedimentos exactos que comienzan a erosionarse, los árboles que bordean las orillas de los canales y el nivel freático que se eleva desde abajo varían según el lugar y el tiempo.

Y todos ellos podría importar. 

Sin embargo, recientemente, una receta fundamental para construir redes de ríos ha comenzado a tomar forma.

Un equipo liderado por Daniel Rothman, geofísico del Instituto de Tecnología de Massachusetts (MIT), ha pasado los últimos años argumentando que un patrón de crecimiento básico y casi ubicuo puede explicar las formas de las redes fluviales excavadas en suelos húmedos y tal vez más allá.

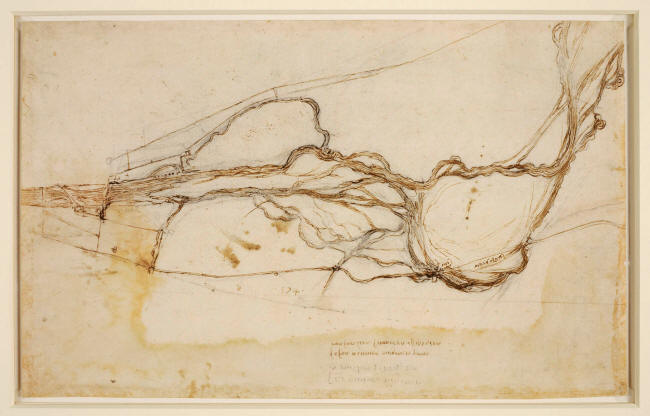
En 1504 Leonardo da Vinci

esbozó el río Arno al oeste de Florencia,

como parte de un estudio de cómo podría ser desviado.
Royal Collection Trust

© Su Majestad la Reina Isabel II 2018

Han llevado a su modelo más allá de la pizarra, al campo y, más recientemente, a través de la tumultuosa y ruidosa totalidad de las cuencas de los ríos de la Tierra.

Ahora están mirando aún más lejos a Marte, y quizás a la luna Titán de Saturno, cada una de las cuales alberga sus propios y misteriosos canales de ramificación.

Su matemática básica no funciona todo el tiempo, pero sí funciona ampliamente. Y donde no funciona, el equipo cree que el desglose proporciona su propio indicio de las condiciones ambientales subyacentes. 
Más allá de todo eso, su receta para redes fluviales también ofrece una cierta calidad estética.

"Las matemáticas son hermosas", dijo Christopher Paola, geólogo de la Universidad de Minnesota, que no formó parte de la investigación.

"Es simplemente hermoso".

Desde Baches a Bifurcaciones

Si Rothman tiene razón, el trabajo de su equipo agregaría redes de ríos, o al menos algunas de ellas, a una clase de patrones de ramificación inquietantemente similares que se encuentran en toda la naturaleza.

Todos estos sistemas siguen lo que los matemáticos llaman el crecimiento de Laplace, llamado así por el matemático francés del siglo dieciocho Pierre-Simon Laplace.

Los copos de nieve, analizados de cerca, parecen brotar de sus estructuras cristalinas de aspecto simétrico a través del crecimiento laplaciano.

El proceso también predice el patrón de ramificación que toma la corriente eléctrica cuando salta a través de una brecha, cómo se propagan las colonias bacterianas en las placas de Petri y cómo los minerales se convierten en patrones venosos y dendríticos que parecen fósiles en las rocas de todo el mundo.
 

Damian McCoig 

En cada uno de ellos, los patrones crecen cuando se desarrolla una protuberancia a partir de una imperfección en un límite por lo demás suave.

Considere la superficie de un copo de nieve recién nacido, un borde congelado que se arrastra hacia el agua ambiental no congelada Invariablemente, lo que comienza como un borde liso tendrá algunos pequeños bultos, incluso unos pocos átomos fuera de lugar.

Ese golpe sobresaldrá un poco en el líquido.

Por ahí, el abultamiento pierde calor en el agua circundante un poco más rápido. Se enfría, y un poco más de agua se congela sobre ella. Con el tiempo el bulto crece, formando un bulto más grande.

El proceso continúa, y pronto la imperfección atómica se extiende en una rama cristalina.

Los detalles varían en diferentes sistemas laplacianos, pero la regla es la misma:

El crecimiento engendra crecimiento. Los bultos forman ramas. Las ramas siguen creciendo en sus puntas.

Eventualmente, las ramas pueden generar sus propios baches a través del mismo proceso. Eso puede hacer que las nuevas ramas copien las mismas formas que las ramas primarias, solo en escalas más pequeñas. 
El equipo de Rothman ha argumentado durante mucho tiempo que ciertas redes de ríos "el abuelo de todos los patrones de ramificación natural obvios" pertenecen a este ilustre grupo.

Pero el problema, para los cazadores de patrones, es mostrar que las reglas simples realmente se trasladan a la realidad desordenada. 

 

Un Río Crece

El grupo de Rothman encontró su prueba de concepto cerca de la ciudad de Bristol en Florida Panhandle. Allí, una vasta red de canales alimenta el agua hacia el río Apalachicola. 
La red en sí misma, que termina en puntas de canales dendríticos, se está extendiendo lentamente lejos del río.

A medida que crecen las puntas de los canales, cortan la arena de 2 millones de años. En cada punta de crecimiento, el agua subterránea sale a la superficie. Al igual que el agua fría alrededor de un copo de nieve en crecimiento, es el tipo de ambiente que se presta al crecimiento laplaciano.

Sobre la base del trabajo sobre la erosión causada por el agua subterránea por Thomas Dunne, un geomorfólogo de la Universidad de California en Santa Bárbara, el equipo de Rothman se propuso probar si las matemáticas simples podían describir esta situación.

Volaron a Florida y se lanzaron a través de estas corrientes, midiendo la velocidad a la que el agua fluye a través de canales individuales.

Luego usaron un radar de penetración en el suelo para verificar la altura del nivel freático debajo.